5.5 Packing and Unpacking Bit Strings
A common bit operation is inserting a bit string into an operand or extracting a bit string from an operand. Previous chapters in this text have provided simple examples of packing and unpacking such data, now it is time to formally describe how to do this.
For the purposes of the current discussion, we will assume that we're dealing with bit strings; that is, a contiguous sequence of bits. A little later in this chapter we'll take a look at how to extract and insert bit sets in an operand. Another simplification we'll make is that the bit string completely fits within a byte, word, or double word operand. Large bit strings that cross object boundaries require additional processing; a discussion of bit strings that cross double word boundaries appears later in this section.
A bit string has two attributes that we must consider when packing and unpacking that bit string: a starting bit position and a length. The starting bit position is the bit number of the L.O. bit of the string in the larger operand. The length, of course, is the number of bits in the operand. To insert (pack) data into a destination operand we will assume that we start with a bit string of the appropriate length that is right-justified (i.e., starts in bit position zero) in an operand and is zero extended to eight, sixteen, or thirty-two bits. The task is to insert this data at the appropriate starting position in some other operand that is eight, sixteen, or thirty-bits wide. There is no guarantee that the destination bit positions contain any particular value.
The first two steps (which can occur in any order) is to clear out the corresponding bits in the destination operand and shift (a copy of) the bit string so that the L.O. bit begins at the appropriate bit position. After completing these two steps, the third step is to OR the shifted result with the destination operand. This inserts the bit string into the destination operand.
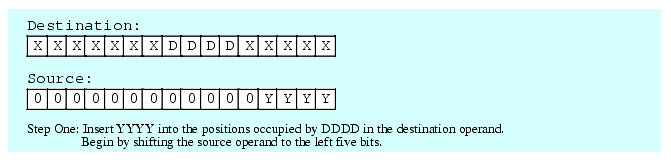
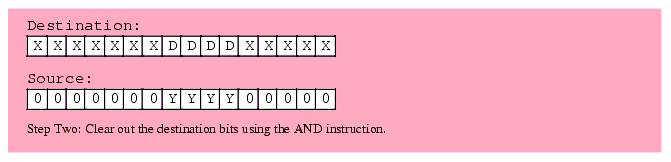
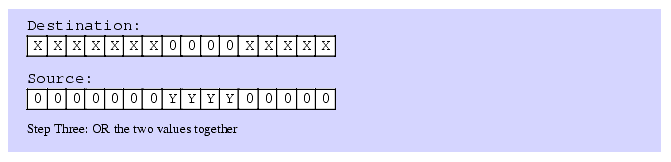
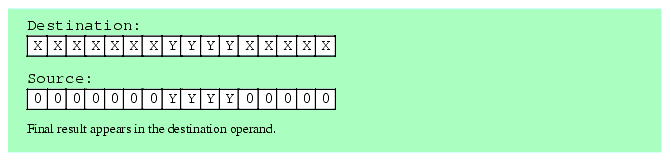
Figure 5.3 Inserting a Bit String Into a Destination Operand
It only takes three instructions to insert a bit string of known length into a destination operand. The following three instructions demonstrate how to handle the insertion operation in Figure 5.3; These instructions assume that the source operand is in BX and the destination operand is AX:
shl( 5, bx ); and( %111111000011111, ax ); or( bx, ax );If the length and the starting position aren't known when you're writing the program (that is, you have to calculate them at run time), then bit string insertion is a little more difficult. However, with the use of a lookup table it's still an easy operation to accomplish. Let's assume that we have two eight-bit values: a starting bit position for the field we're inserting and a non-zero eight-bit length value. Also assume that the source operand is in EBX and the destination operand is EAX. The code to insert one operand into another could take the following form:
readonly // The index into the following table specifies the length of the bit string // at each position: MaskByLen: dword[ 32 ] := [ 0, $1, $3, $7, $f, $1f, $3f, $7f, $ff, $1ff, $3ff, $7ff, $fff, $1fff, $3fff, $7fff, $ffff, $1_ffff, $3_ffff, $7_ffff, $f_ffff, $1f_ffff, $3f_ffff, $7f_ffff, $ff_ffff, $1ff_ffff, $3ff_ffff, $7ff_ffff, $fff_ffff, $1fff_ffff, $3fff_ffff, $7fff_ffff, $ffff_ffff ]; . . . movzx( Length, edx ); mov( MaskByLen[ edx*4 ], edx ); mov( StartingPosition, cl ); shl( cl, edx ); not( edx ); shl( cl, ebx ); and( edx, eax ); or( ebx, eax );Each entry in the MaskByLen table contains the number of one bits specified by the index into the table. Using the Length value as an index into this table fetches a value that has as many one bits as the Length value. The code above fetches an appropriate mask, shifts it to the left so that the L.O. bit of this run of ones matches the starting position of the field into which we want to insert the data, then it inverts the mask and uses the inverted value to clear the appropriate bits in the destination operand.
To extract a bit string from a larger operand is just as easy as inserting a bit string into some larger operand. All you've got to do is mask out the unwanted bits and then shift the result until the L.O. bit of the bit string is in bit zero of the destination operand. For example, to extract the four-bit field starting at bit position five in EBX and leave the result in EAX, you could use the following code:
mov( ebx, eax ); // Copy data to destination. and( %1_1110_0000, ebx ); // Strip unwanted bits. shr( 5, eax ); // Right justify to bit position zero.If you do not know the bit string's length and starting position when you're writing the program, you can still extract the desired bit string. The code is very similar to insertion (though a tiny bit simpler). Assuming you have the Length and StartingPosition values we used when inserting a bit string, you can extract the corresponding bit string using the following code (assuming source=EBX and dest=EAX):
movzx( Length, edx ); mov( MaskByLen[ edx*4 ], edx ); mov( StartingPosition, cl ); mov( ebx, eax ); shr( cl, eax ); and( edx, eax );The examples up to this point all assume that the bit string appears completely within a double word (or smaller) object. This will always be the case if the bit string is less than or equal to 24 bits in length. However, if the length of the bit string plus its starting position (mod eight) within an object is greater than 32, then the bit string will cross a double word boundary within the object. To extract such bit strings requires up to three operations: one operation to extract the start of the bit string (up to the first double word boundary), an operation that copies whole double words (assuming the bit string is so long that it consumes several double words), and a final operation that copies left-over bits in the last double word at the end of the bit string. The actual implementation of this operation is left as an exercise at the end of this volume.
5.6 Coalescing Bit Sets and Distributing Bit Strings
Inserting and extracting bit sets is little different than inserting and extract bit strings if the "shape" of the bit set you're inserting (or resulting bit set you're extracting) is the same as the bit set in the main object. The "shape" of a bit set is the distribution of the bits in the set, ignoring the starting bit position of the set. So a bit set that includes bits zero, four, five, six, and seven has the same shape as a bit set that includes bits 12, 16, 17, 18, and 19 since the distribution of the bits is the same. The code to insert or extract this bit set is nearly identical to that of the previous section; the only difference is the mask value you use. For example, to insert this bit set starting at bit number zero in EAX into the corresponding bit set starting at position 12 in EBX, you could use the following code:
and( %1111_0001_0000_0000_0000, ebx ); // Mask out destination bits. shl( 12, eax ); // Move source bits into posn. or( eax, ebx ); // Merge the bit set into EBX.However, suppose you have five bits in bit positions zero through four in EAX and you want to merge them into bits 12, 16, 17, 18, and 19 in EBX. Somehow you've got to distribute the bits in EAX prior to logically ORing the values into EBX. Given the fact that this particular bit set has only two runs of one bits, the process is somewhat simplified, the following code achieves this in a somewhat sneaky fashion:
and( %1111_0001_0000_0000_0000, ebx ); shl( 3, eax ); // Spread out the bits: 1-4 goes to 4-7 and 0 to 3. btr( 3, eax ); // Bit 3->carry and then clear bit 3 rcl( 12, eax ); // Shift in carry and put bits into final position or( eax, ebx ); // Merge the bit set into EBX.This trick with the BTR (bit test and reset) instruction worked well because we only had one bit out of place in the original source operand. Alas, had the bits all been in the wrong location relative to one another, this scheme might not have worked quite as well. We'll see a more general solution in just a moment.
Extracting this bit set and collecting ("coalescing") the bits into a bit string is not quite as easy. However, there are still some sneaky tricks we can pull. Consider the following code that extracts the bit set from EBX and places the result into bits 0..4 of EAX:
mov( ebx, eax ); and( %1111_0001_0000_0000_0000, eax ); // Strip unwanted bits. shr( 5, eax ); // Put bit 12 into bit 7, etc. shr( 3, ah ); // Move bits 11..14 to 8..11. shr( 7, eax ); // Move down to bit zero.This code moves (original) bit 12 into bit position seven, the H.O. bit of AL. At the same time it moves bits 16..19 down to bits 11..14 (bits 3..6 of AH). Then the code shifts the bits 3..6 in AH down to bit zero. This positions the H.O. bits of the bit set so that they are adjacent to the bit left in AL. Finally, the code shifts all the bits down to bit zero. Again, this is not a general solution, but it shows a clever way to attack this problem if you think about it carefully.
The problem with the coalescing and distribution algorithms above is that they are not general. They apply only to their specific bit sets. In general, specific solutions are going to provide the most efficient solution. A generalized solution (perhaps that lets you specify a mask and the code distributes or coalesces the bits accordingly) is going to be a bit more difficult. The following code demonstrates how to distribute the bits in a bit string according to the values in a bit mask:
// EAX- Originally contains some value into which we insert bits from EBX. // EBX- L.O. bits contain the values to insert into EAX. // EDX- bitmap with ones indicating the bit positions in EAX to insert. // CL- Scratchpad register. mov( 32, cl ); // Count # of bits we rotate. jmp DistLoop; CopyToEAX: rcr( 1, ebx ); // Don't use SHR here, must preserve Z-flag. rcr( 1, eax ); jz Done; DistLoop: dec( cl ); shr( 1, edx ); jc CopyToEAX; ror( 1, eax ); // Keep current bit in EAX. jnz DistLoop; Done: ror( cl, eax ); // Reposition remaining bits.In the code above, if we load EDX with %1100_1001 then this code will copy bits 0..3 to bits 0, 3, 6, and 7 in EAX. Notice the short circuit test that checks to see if we've exhausted the values in EDX (by checking for a zero in EDX). Note that the rotate instructions do not affect the zero flag while the shift instructions do. Hence the SHR instruction above will set the zero flag when there are no more bits to distribute (i.e., when EDX becomes zero).
The general algorithm for coalescing bits is a tad more efficient than distribution. Here's the code that will extract bits from EBX via the bit mask in EDX and leave the result in EAX:
// EAX- Destination register. // EBX- Source register. // EDX- Bitmap with ones representing bits to copy to EAX. // EBX and EDX are not preserved. sub( eax, eax ); // Clear destination register. jmp ShiftLoop; ShiftInEAX: rcl( 1, ebx ); // Up here we need to copy a bit from rcl( 1, eax ); // EBX to EAX. ShiftLoop: shl( 1, edx ); // Check mask to see if we need to copy a bit. jc ShiftInEAX; // If carry set, go copy the bit. rcl( 1, ebx ); // Current bit is uninteresting, skip it. jnz ShiftLoop; // Repeat as long as there are bits in EDX.This sequence takes advantage of one sneaky trait of the shift and rotate instructions: the shift instructions affect the zero flag while the rotate instructions do not. Therefore, the "shl( 1, edx);" instruction sets the zero flag when EDX becomes zero (after the shift). If the carry flag was also set, the code will make one additional pass through the loop in order to shift a bit into EAX, but the next time the code shifts EDX one bit to the left, EDX is still zero and so the carry will be clear. On this iteration, the code falls out of the loop.
Another way to coalesce bits is via table lookup. By grabbing a byte of data at a time (so your tables don't get too large) you can use that byte's value as an index into a lookup table that coalesces all the bits down to bit zero. Finally, you can merge the bits at the low end of each byte together. This might produce a more efficient coalescing algorithm in certain cases. The implementation is left to the reader...
5.7 Packed Arrays of Bit Strings
Although it is far more efficient to create arrays whose elements' have an integral number of bytes, it is quite possible to create arrays of elements whose size is not a multiple of eight bits. The drawback is that calculating the "address" of an array element and manipulating that array element involves a lot of extra work. In this section we'll take a look at a few examples of packing and unpacking array elements in an array whose elements are an arbitrary number of bits long.
Before proceeding, it's probably worthwhile to discuss why you would want to bother with arrays of bit objects. The answer is simple: space. If an object only consumes three bits, you can get 2.67 times as many elements into the same space if you pack the data rather than allocating a whole byte for each object. For very large arrays, this can be a substantial savings. Of course, the cost of this space savings is speed: you've got to execute extra instructions to pack and unpack the data, thus slowing down access to the data.
The calculation for locating the bit offset of an array element in a large block of bits is almost identical to the standard array access; it is
Element_Address_in_bits = Base_address_in_bits + index * element_size_in_bits
Once you calculate the element's address in bits, you need to convert it to a byte address (since we have to use byte addresses when accessing memory) and extract the specified element. Because the base address of an array element (almost) always starts on a byte boundary, we can use the following equations to simplify this task:
Byte_of_1st_bit = Base_Address + (index * element_size_in_bits )/8 Offset_to_1st_bit = (index * element_size_in_bits) % 8 (note "%" = MOD)For example, suppose we have an array of 200 three-bit objects that we declare as follows:
static AO3Bobjects: byte[ (200*3)/8 + 1 ]; // "+1" handles trucation.The constant expression in the dimension above reserves space for enough bytes to hold 600 bits (200 elements, each three bits long). As the comment notes, the expression adds an extra byte at the end to ensure we don't lose any odd bits (that won't happen in this example since 600 is evenly divisible by 8, but in general you can't count on this; one extra byte usually won't hurt things).
Now suppose you want to access the ith three-bit element of this array. You can extract these bits by using the following code:
// Extract the ith group of three bits in AO3Bobjects and leave this value // in EAX. sub( ecx, ecx ); // Put i/8 remainder here. mov( i, eax ); // Get the index into the array. shrd( 3, eax, ecx ); // EAX/8 -> EAX and EAX mod 8 -> ECX (H.O. bits) shr( 3, eax ); // Remember, shrd above doesn't modify eax. rol( 3, ecx ); // Put remainder into L.O. three bits of ECX. // Okay, fetch the word containing the three bits we want to extract. // We have to fetch a word because the last bit or two could wind up // crossing the byte boundary (i.e., bit offset six and seven in the // byte). mov( AO3Bobjecs[eax], eax ); shr( cl, eax ); // Move bits down to bit zero. and( %111, eax ); // Remove the other bits.Inserting an element into the array is a bit more difficult. In addition to computing the base address and bit offset of the array element, you've also got to create a mask to clear out the bits in the destination where you're going to insert the new data. The following code inserts the L.O. three bits of EAX into the ith element of the AO3Bobjects array.
// Insert the L.O. three bits of AX into the ith element of AO3Bobjects: readonly Masks: word[8] := [ !%0000_0111, !%0000_1110, !%0001_1100, !%0011_1000, !%0111_0000, !%1110_0000, !%1_1100_0000, !%11_1000_0000 ]; . . . sub( ecx, ecx ); // Put remainder here. mov( i, ebx ); // Get the index into the array. shrd( 3, ebx, ecx ); // i/8 -> EBX, i % 8 -> ECX. shr( 3, ebx ); rol( 3, ecx ); and( %111, ax ); // Clear unneeded bits from AX. mov( Masks[ecx], dx ); // Mask to clear out our array element. and( AO3Bobjects[ ebx ], dx ); // Grab the bits and clear those // we're inserting. shl( cl, ax ); // Put our three bits in their proper location. or( ax, dx ); // Merge bits into destination. mov( dx, AO3Bobjects[ ebx ] ); // Store back into memory.Notice the use of a lookup table to generate the masks needed to clear out the appropriate position in the array. Each element of this array contains all ones except for three zeros in the position we need to clear for a given bit offset (note the use of the "!" operator to invert the constants in the table).
5.8 Searching for a Bit
A very common bit operation is to locate the end of some run of bits. A very common special case of this operation is to locate the first (or last) set or clear bit in a 16- or 32-bit value. In this section we'll explore ways to accomplish this.
Before describing how to search for the first or last bit of a given value, perhaps it's wise to discuss exactly what the terms "first" and "last" mean in this context. The term "first set bit" means the first bit in a value, scanning from bit zero towards the high order bit, that contains a one. A similar definition exists for the "first clear bit." The "last set bit" is the first bit in a value, scanning from the high order bit towards bit zero, that contains a one. A similar definition exists for the last clear bit.
One obvious way to scan for the first or last bit is to use a shift instruction in a loop and count the number of iterations before you shift out a one (or zero) into the carry flag. The number of iterations specifies the position. Here's some sample code that checks for the first set bit in EAX and returns that bit position in ECX:
mov( -32, ecx ); // Count off the bit positions in ECX. TstLp: shr( 1, eax ); // Check to see if current bit position contains jc Done // a one; exit loop if it does. inc( ecx ); // Bump up our bit counter by one. jnz TstLp; // Exit if we execute this loop 32 times. Done: add( 32, cl ); // Adjust loop counter so it holds the bit posn. // At this point, ECX contains the bit position of the first set bit. // ECX contains 32 if EAX originally contained zero (no set bits).The only thing tricky about this code is the fact that it runs the loop counter from -32 to zero rather than 32 down to zero. This makes it slightly easier to calculate the bit position once the loop terminates.
The drawback to this particular loop is that it's expensive. This loop repeats as many as 32 times depending on the original value in EAX. If the values you're checking often have lots of zeros in the L.O. bits of EAX, this code runs rather slow.
Searching for the first (or last) set bit is such a common operation that Intel added a couple of instructions on the 80386 specifically to accelerate this process. These instructions are BSF (bit scan forward) and BSR (bit scan reverse). Their syntax is as follows:
bsr( source, destReg ); bsf( source, destReg );The source and destinations operands must be the same size and they must both be 16- or 32-bit objects. The destination operand has to be a register, the source operand can be a register or a memory location.
The BSF instruction scans for the first set bit (starting from bit position zero) in the source operand. The BSR instruction scans for the last set bit in the source operand by scanning from the H.O. bit towards the L.O. bit. If these instructions find a bit that is set in the source operand then they clear the zero flag and put the bit position into the destination register. If the source register contains zero (i.e., there are no set bits) then these instructions set the zero flag and leave an indeterminate value in the destination register. Note that you should test the zero flag immediately after the execution of these instructions to validate the destination register's value. Examples:
mov( SomeValue, ebx ); // Value whose bits we want to check. bsf( ebx. eax ); // Put position of first set bit in EAX. jz NoBitsSet; // Branch if SomeValue contains zero. mov( eax, FirstBit ); // Save location of first set bit. . . .You use the BSR instruction in an identical fashion except that it computes the bit position of the last set bit in an operand (that is, the first set bit it finds when scanning from the H.O. bit towards the L.O. bit).
The 80x86 CPUs do not provide instructions to locate the first bit containing a zero. However, you can easily scan for a zero bit by first inverting the source operand (or a copy of the source operand if you must preserve the source operand's value). If you invert the source operand, then the first "1" bit you find corresponds to the first zero bit in the original operand value.
The BSF and BSR instructions are complex instructions (i.e., they are not a part of the 80x86 "RISC core" instruction set). Therefore, these instructions are necessarily as fast as other instructions. Indeed, in some circumstances it may be faster to locate the first set bit using discrete instructions. However, since the execution time of these instructions varies widely from CPU to CPU, you should first test the performance of these instructions prior to using them in time critical code.
Note that the BSF and BSR instructions do not affect the source operand. A common operation is to extract the first (or last) set bit you find in some operand. That is, you might want to clear the bit once you find it. If the source operand is a register (or you can easily move it into a register) then you can use the BTR (or BTC) instruction to clear the bit once you've found it. Here's some code that achieves this result:
bsf( eax, ecx ); // Locate first set bit in EAX. if( @nz ) then // If we found a bit, clear it. btr( ecx, eax ); // Clear the bit we just found. endif;At the end of this sequence, the zero flag indicates whether we found a bit (note that BTR does not affect the zero flag). Alternately, you could add an ELSE section to the IF statement above that handles the case when the source operand (EAX) contains zero at the beginning of this instruction sequence.
Since the BSF and BSR instructions only support 16- and 32-bit operands, you will have to compute the first bit position of an eight-bit operand a little differently. There are a couple of reasonable approaches. First, of course, you can usually zero extend an eight-bit operand to 16 or 32 bits and then use the BSF or BSR instructions on this operand. Another alternative is to create a lookup table where each entry in the table contains the number of bits in the value you use as an index into the table; then you can use the XLAT instruction to "compute" the first bit position in the value (note that you will have to handle the value zero as a special case). Another solution is to use the shift algorithm appearing at the beginning of this section; for an eight-bit operand, this is not an entirely inefficient solution.
One interesting use of the BSF and BSR instructions is to "fill in" a character set with all the values from the lowest-valued character in the set through the highest-valued character. For example, suppose a character set contains the values {`A', `M', `a'..'n', `z'}; if we filled in the gaps in this character set we would have the values {`A'..'z'}. To compute this new set we can use BSF to determine the ASCII code of the first character in the set and BSR to determine the ASCII code of the last character in the set. After doing this, we can feed those two ASCII codes to the cs.rangeChar function to compute the new set.
You can also use the BSF and BSR instructions to determine the size of a run of bits, assuming that you have a single run of bits in your operand. Simply locate the first and last bits in the run (as above) and the compute the difference (plus one) of the two values. Of course, this scheme is only valid if there are no intervening zeros between the first and last set bits in the value.
5.9 Counting Bits
The last example in the previous section demonstrates a specific case of a very general problem: counting bits. Unfortunately, that example has a severe limitation: it only counts a single run of one bits appearing in the source operand. This section discusses a more general solution to this problem.
Hardly a week goes by that someone doesn't ask how to count the number of bits in a register operand on one of the Internet news groups. This is a common request, undoubtedly, because many assembly language course instructors assign this task a project to their students as a way to teach them about the shift and rotate instructions. Undoubtedly, the solution these instructor expect is something like the following:
// BitCount1: // // Counts the bits in the EAX register, returning the count in EBX. mov( 32, cl ); // Count the 32 bits in EAX. sub( ebx, ebx ); // Accumulate the count here. CntLoop: shr( 1, eax ); // Shift next bit out of EAX and into Carry. adc( 0, bl ); // Add the carry into the EBX register. dec( cl ); // Repeat 32 times. jnz CntLoopThe "trick" worth noting here is that this code uses the ADC instruction to add the value of the carry flag into the BL register. Since the count is going to be less than 32, the result will fit comfortably into BL. This code uses "adc( 0, bl );" rather than "adc( 0, ebx );" because the former instruction is smaller.
Tricky code or not, this instruction sequence is not particularly fast. As you can tell with just a small amount of analysis, the loop above always executes 32 times, so this code sequence executes 130 instructions (four instructions per iteration plus two extra instructions). One might ask if there is a more efficient solution, the answer is yes. The following code, taken from the AMD Athlon optimization guide, provides a faster solution (see the comments for a description of the algorithm):
// bitCount- // // Counts the number of "1" bits in a dword value. // This function returns the dword count value in EAX. procedure bits.cnt( BitsToCnt:dword ); nodisplay; const EveryOtherBit := $5555_5555; EveryAlternatePair := $3333_3333; EvenNibbles := $0f0f_0f0f; begin cnt; push( edx ); mov( BitsToCnt, eax ); mov( eax, edx ); // Compute sum of each pair of bits // in EAX. The algorithm treats // each pair of bits in EAX as a two // bit number and calculates the // number of bits as follows (description // is for bits zero and one, it generalizes // to each pair): // // EDX = BIT1 BIT0 // EAX = 0 BIT1 // // EDX-EAX = 00 if both bits were zero. // 01 if Bit0=1 and Bit1=0. // 01 if Bit0=0 and Bit1=1. // 10 if Bit0=1 and Bit1=1. // // Note that the result is left in EDX. shr( 1, eax ); and( EveryOtherBit, eax ); sub( eax, edx ); // Now sum up the groups of two bits to // produces sums of four bits. This works // as follows: // // EDX = bits 2,3, 6,7, 10,11, 14,15, ..., 30,31 // in bit positions 0,1, 4,5, ..., 28,29 with // zeros in the other positions. // // EAX = bits 0,1, 4,5, 8,9, ... 28,29 with zeros // in the other positions. // // EDX+EAX produces the sums of these pairs of bits. // The sums consume bits 0,1,2, 4,5,6, 8,9,10, ... 28,29,30 // in EAX with the remaining bits all containing zero. mov( edx, eax ); shr( 2, edx ); and( EveryAlternatePair, eax ); and( EveryAlternatePair, edx ); add( edx, eax ); // Now compute the sums of the even and odd nibbles in the // number. Since bits 3, 7, 11, etc. in EAX all contain // zero from the above calcuation, we don't need to AND // anything first, just shift and add the two values. // This computes the sum of the bits in the four bytes // as four separate value in EAX (AL contains number of // bits in original AL, AH contains number of bits in // original AH, etc.) mov( eax, edx ); shr( 4, eax ); add( edx, eax ); and( EvenNibbles, eax ); // Now for the tricky part. // We want to compute the sum of the four bytes // and return the result in EAX. The following // multiplication achieves this. It works // as follows: // (1) the $01 component leaves bits 24..31 // in bits 24..31. // // (2) the $100 component adds bits 17..23 // into bits 24..31. // // (3) the $1_0000 component adds bits 8..15 // into bits 24..31. // // (4) the $1000_0000 component adds bits 0..7 // into bits 24..31. // // Bits 0..23 are filled with garbage, but bits // 24..31 contain the actual sum of the bits // in EAX's original value. The SHR instruction // moves this value into bits 0..7 and zeroes // out the H.O. bits of EAX. intmul( $0101_0101, eax ); shr( 24, eax ); pop( edx ); end cnt;5.10 Reversing a Bit String
Another common programming project instructions assign, and a useful function in its own right, is a program that reverses the bits in an operand. That is, it swaps the L.O. bit with the H.O. bit, bit #1 with the next-to-H.O. bit, etc. The typical solution an instructor probably expects for this assignment is the following:
// Reverse the 32-bits in EAX, leaving the result in EBX: mov( 32, cl ); RvsLoop: shr( 1, eax ); // Move current bit in EAX to the carry flag. rcl( 1, ebx ); // Shift the bit back into EBX, backwards. dec( cl ); jnz RvsLoopAs with the previous examples, this code suffers from the fact that it repeats the loop 32 times for a grand total of 129 instructions. By unrolling the loop you can get it down to 64 instructions, but this is still somewhat expensive.
As usual, the best solution to an optimization problem is often a better algorithm rather than attempting to tweak your code by trying to choose faster instructions to speed up some code. However, a little intelligence goes a long way when manipulating bits. In the last section, for example, we were able to speed up counting the bits in a string by substituting a more complex algorithm for the simplistic "shift and count" algorithm. In the example above, we are once again faced with a very simple algorithm with a loop that repeats for one bit in each number. The question is: "Can we discover an algorithm that doesn't execute 129 instructions to reverse the bits in a 32-bit register?" The answer is "yes" and the trick is to do as much work as possible in parallel.
Suppose that all we wanted to do was swap the even and odd bits in a 32-bit value. We can easily swap the even an odd bits in EAX using the following code:
mov( eax, edx ); // Make a copy of the odd bits in the data. shr( 1, eax ); // Move the even bits to the odd positions. and( $5555_5555, edx ); // Isolate the odd bits by clearing even bits. and( $5555_5555, eax ); // Isolate the even bits (in odd posn now). shl( 1, edx ); // Move the odd bits to the even positions. or( edx, eax ); // Merge the bits and complete the swap.Of course, swapping the even and odd bits, while somewhat interesting, does not solve our larger problem of reversing all the bits in the number. But it does take us part of the way there. For example, if after executing the code sequence above, we swap adjacent pairs of bits, then we've managed to swap the bits in all the nibbles in the 32-bit value. Swapping adjacent pairs of bits is done in a manner very similar to the above, the code is
mov( eax, edx ); // Make a copy of the odd numbered bit pairs. shr( 2, eax ); // Move the even bit pairs to the odd posn. and( $3333_3333, edx ); // Isolate the odd pairs by clearing even pairs. and( $3333_3333, eax ); // Isolate the even pairs (in odd posn now). shl( 2, edx ); // Move the odd pairs to the even positions. or( edx, eax ); // Merge the bits and complete the swap.After completing the sequence above we swap the adjacent nibbles in the 32-bit register. Again, the only difference is the bit mask and the length of the shifts. Here's the code:
mov( eax, edx ); // Make a copy of the odd numbered nibbles. shr( 4, eax ); // Move the even nibbles to the odd position. and( $0f0f_0f0f, edx ); // Isolate the odd nibbles. and( $0f0f_0f0f, eax ); // Isolate the even nibbles (in odd posn now). shl( 4, edx ); // Move the odd pairs to the even positions. or( edx, eax ); // Merge the bits and complete the swap.You can probably see the pattern developing and can figure out that in the next two steps we've got to swap the bytes and then the words in this object. You can use code like the above, but there is a better way - use the BSWAP instruction. The BSWAP (byte swap) instruction uses the following syntax:
bswap( reg32 );This instruction swaps bytes zero and three and it swaps bytes one and two in the specified 32-bit register. The principle use of this instruction is to convert data between the so-called "little endian" and "big-endian" data formats1. Although we don't specifically need this instruction for this purpose here, the BSWAP instruction does swap the bytes and words in a 32-bit object exactly the way we want them when reversing bits, so rather than sticking in another 12 instructions to swap the bytes and then the words, we can simply use a "bswap( eax );" instruction to complete the job after the instructions above. The final code sequence is
mov( eax, edx ); // Make a copy of the odd bits in the data. shr( 1, eax ); // Move the even bits to the odd positions. and( $5555_5555, edx ); // Isolate the odd bits by clearing even bits. and( $5555_5555, eax ); // Isolate the even bits (in odd posn now). shl( 1, edx ); // Move the odd bits to the even positions. or( edx, eax ); // Merge the bits and complete the swap. mov( eax, edx ); // Make a copy of the odd numbered bit pairs. shr( 2, eax ); // Move the even bit pairs to the odd posn. and( $3333_3333, edx ); // Isolate the odd pairs by clearing even pairs. and( $3333_3333, eax ); // Isolate the even pairs (in odd posn now). shl( 2, edx ); // Move the odd pairs to the even positions. or( edx, eax ); // Merge the bits and complete the swap. mov( eax, edx ); // Make a copy of the odd numbered nibbles. shr( 4, eax ); // Move the even nibbles to the odd position. and( $0f0f_0f0f, edx ); // Isolate the odd nibbles. and( $0f0f_0f0f, eax ); // Isolate the even nibbles (in odd posn now). shl( 4, edx ); // Move the odd pairs to the even positions. or( edx, eax ); // Merge the bits and complete the swap. bswap( eax ); // Swap the bytes and words.This algorithm only requires 19 instructions and it executes much faster than the bit shifting loop appearing earlier. Of course, this sequence does consume a bit more memory, so if you're trying to save memory rather than clock cycles, the loop is probably a better solution.
5.11 Merging Bit Strings
Another common bit string operation is producing a single bit string by merging, or interleaving, bits from two different sources. The following example code sequence creates a 32-bit string by merging alternate bits from two 16-bit strings:
// Merge two 16-bit strings into a single 32-bit string. // AX - Source for even numbered bits. // BX - Source for odd numbered bits. // CL - Scratch register. // EDX- Destination register. mov( 16, cl ); MergeLp: shrd( 1, eax, edx ); // Shift a bit from EAX into EDX. shrd( 1, ebx, edx ); // Shift a bit from EBX into EDX. dec( cl ); jne MergeLp;This particular example merged two 16-bit values together, alternating their bits in the result value. For a faster implementation of this code, unrolling the loop is probably you're best bet since this eliminates half the instructions that execute on each iteration of the loop above.
With a few slight modifications, we could also have merged four eight-bit values together, or we could have generated the result using other bit sequences; for example, the following code copies bits 0..5 from EAX, then bits 0..4 from EBX, then bits 6..11 from EAX, then bits 5..15 from EBX, and finally bits 12..15 from EAX:
shrd( 6, eax, edx ); shrd( 5, ebx, edx ); shrd( 6, eax, edx ); shrd( 11, ebx, edx ); shrd( 4, eax, edx );5.12 Extracting Bit Strings
Of course, we can easily accomplish the converse of merging two bit streams; i.e., we can extract and distribute bits in a bit string among multiple destinations. The following code takes the 32-bit value in EAX and distributes alternate bits among the BX and DX registers:
mov( 16, cl ); // Count off the number of loop iterations. ExtractLp: ` shr( 1, eax ); // Extract even bits to (E)BX. rcr( 1, ebx ); shr( 1, eax ); // Extract odd bits to (E)DX. rcr( 1, edx ); dec( cl ); // Repeat 16 times. jnz ExtractLp; shr( 16, ebx ); // Need to move the results from the H.O. shr( 16, edx ); // bytes of EBX/EDX to the L.O. bytes.This sequence executes 99 instructions. This isn't terrible, but we can probably do a little better by using a better algorithm that extracts bits in parallel. Employing the technique we used to reverse bits in a register, we can come up with the following algorithm that relocates all the even bits to the L.O. word of EAX and all the odd bits to the H.O. word of EAX.
// Swap bits at positions (1,2), (5,6), (9,10), (13,14), (17,18), // (21,22), (25,26), and (29, 30). mov( eax, edx ); and( $9999_9999, eax ); // Mask out the bits we'll keep for now. mov( edx, ecx ); shr( 1, edx ); // Move 1st bits in tuple above to the and( $2222_2222, ecx ); // correct position and mask out the and( $2222_2222, edx ); // unneeded bits. shl( 1, ecx ); // Move 2nd bits in tuples above. or( edx, ecx ); // Merge all the bits back together. or( ecx, eax ); // Swap bit pairs at positions ((2,3), (4,5)), ((10,11), (12,13)), etc. mov( eax, edx ); and( $c3c3_c3c3, eax ); // The bits we'll leave alone. mov( edx, ecx ); shr( 2, edx ); and( $0c0c_0c0c, ecx ); and( $0c0c_0c0c, edx ); shl( 2, ecx ); or( edx, ecx ); or( ecx, eax ); // Swap nibbles at nibble positions (1,2), (5,6), (9,10), etc. mov( eax, edx ); and( $f00f_f00f, eax ); mov( edx, ecx ); shr(4, edx ); and( $0f0f_0f0f, ecx ); and( $0f0f_0f0f, ecx ); shl( 4, ecx ); or( edx, ecx ); or( ecx, eax ); // Swap bits at positions 1 and 2. ror( 8, eax ); xchg( al, ah ); rol( 8, eax );This sequence require 30 instructions. At first blush it looks like a winner since the original loop executes 64 instructions. However, this code isn't quite as good as it looks. After all, if we're willing to write this much code, why not unroll the loop above 16 times? That sequence only requires 64 instructions. So the complexity of the previous algorithm may not gain much on instruction count. As to which sequence is faster, well, you'll have to time them to figure this out. However, the SHRD instructions are not particularly fast, neither are the instructions in the other sequence. This example does not appear here to show you a better algorithm, but rather to demonstrate that writing really tricky code doesn't always provide a big performance boost.
Extracting other bit combinations is left as an exercise for the reader.
5.13 Searching for a Bit Pattern
Another bit-related operation you may need is the ability to search for a particular bit pattern in a string of bits. For example, you might want to locate the bit index of the first occurrence of %1011 starting at some particular position in a bit string. In this section we'll explore some simple algorithms to accomplish this task.
To search for a particular bit pattern we're going to need to know four things: (1) the pattern to search for (the pattern), (2) the length of the pattern we're searching for, (3) the bit string that we're going to search through (the source), and (4) the length of the bit string to search through. The basic idea behind the search is to create a mask based on the length of the pattern and mask a copy of the source with this value. Then we can directly compare the pattern with the masked source for equality. If they are equal, we're done; if they're not equal, then increment a bit position counter, shift the source one position to the right, and try again. We repeat this operation length(source) - length(pattern) times. The algorithm fails if it does not detect the bit pattern after this many attempts (since we will have exhausted all the bits in the source operand that could match the pattern's length). Here's a simple algorithm that searches for a four-bit pattern throughout the EBX register:
mov( 28, cl ); // 28 attempts since 32-4 = 28 (len(src)-len(pat)). mov( %1111, ch ); // Mask for the comparison. mov( pattern, al ); // Pattern to search for. and( ch, al ); // Mask unnecessary bits in AL. mov( source, ebx ); // Get the source value. ScanLp: mov( bl, dl ); // Make a copy of the L.O. four bits of EBX and( ch, dl ); // Mask unwanted bits. cmp( dl, al ); // See if we match the pattern. jz Matched; dec( cl ); // Repeat the specified number of times. jnz ScanLp; << If we get to this point, we failed to match the bit string >> jmp Done; Matched: << If we get to this point, we matched the bit string. We can >> << compute the position in the original source as 28-cl. >> Done:Bit string scanning is a special case of string matching. String matching is a well studied problem in Computer Science and many of the algorithms you can use for string matching are applicable to bit string matching as well. Such algorithms are a bit beyond the scope of this chapter, but to give you a preview of how this works, you compute some function (like XOR or SUB) between the pattern and the current source bits and use the result as an index into a lookup table to determine how many bits you can skip. Such algorithms let you skip several bits rather than only shifting once per each iteration of the scanning loop (as is done by the algorithm above). For more details on string scanning and their possible application to bit string matching, see the appropriate chapter in the volume on Advanced String Handling.
1In the little endian system, which the native 80x86 format, the L.O. byte of an object appears at the lowest address in memory. In the big endian system, which various RISC processors use, the H.O. byte of an object appears at the lowest address in memory. The BSWAP instruction converts between these two data formats.
|