Chapter Four Arrays
4.1 Chapter Overview
This chapter discusses how to declare and use arrays in your assembly language programs. This is probably the most important chapter on composite data structures in this text. Even if you elect to skip the chapters on Strings, Character Sets, Records, and Dates and Times, be sure you read and understand the material in this chapter. Much of the rest of the text depends on your understanding of this material.
4.2 Arrays
Along with strings, arrays are probably the most commonly used composite data type. Yet most beginning programmers have a very weak understanding of how arrays operate and their associated efficiency trade-offs. It's surprising how many novice (and even advanced!) programmers view arrays from a completely different perspective once they learn how to deal with arrays at the machine level.
Abstractly, an array is an aggregate data type whose members (elements) are all the same type. Selection of a member from the array is by an integer index1. Different indices select unique elements of the array. This text assumes that the integer indices are contiguous (though this is by no means required). That is, if the number x is a valid index into the array and y is also a valid index, with x < y, then all i such that x < i < y are valid indices into the array.
Whenever you apply the indexing operator to an array, the result is the specific array element chosen by that index. For example, A[i] chooses the ith element from array A. Note that there is no formal requirement that element i be anywhere near element i+1 in memory. As long as A[i] always refers to the same memory location and A[i+1] always refers to its corresponding location (and the two are different), the definition of an array is satisfied.
In this text, we will assume that array elements occupy contiguous locations in memory. An array with five elements will appear in memory as shown in Figure 4.1
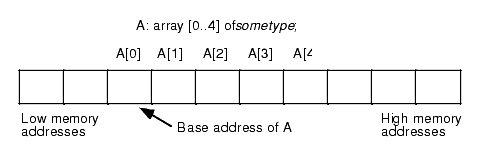
Figure 4.1 Array Layout in Memory
The base address of an array is the address of the first element on the array and always appears in the lowest memory location. The second array element directly follows the first in memory, the third element follows the second, etc. Note that there is no requirement that the indices start at zero. They may start with any number as long as they are contiguous. However, for the purposes of discussion, it's easier to discuss accessing array elements if the first index is zero. This text generally begins most arrays at index zero unless there is a good reason to do otherwise. However, this is for consistency only. There is no efficiency benefit one way or another to starting the array index at zero.
To access an element of an array, you need a function that translates an array index to the address of the indexed element. For a single dimension array, this function is very simple. It is
Element_Address = Base_Address + ((Index - Initial_Index) * Element_Size)where Initial_Index is the value of the first index in the array (which you can ignore if zero) and the value Element_Size is the size, in bytes, of an individual element of the array.
4.3 Declaring Arrays in Your HLA Programs
Before you access elements of an array, you need to set aside storage for that array. Fortunately, array declarations build on the declarations you've seen thus far. To allocate n elements in an array, you would use a declaration like the following in one of the variable declaration sections:
ArrayName: basetype[n];ArrayName is the name of the array variable and basetype is the type of an element of that array. This sets aside storage for the array. To obtain the base address of the array, just use ArrayName.
The "[n]" suffix tells HLA to duplicate the object n times. Now let's look at some specific examples:
static CharArray: char[128]; // Character array with elements 0..127. IntArray: integer[ 8 ]; // "integer" array with elements 0..7. ByteArray: byte[10]; // Array of bytes with elements 0..9. PtrArray: dword[4]; // Array of double words with elements 0..3.The second example, of course, assumes that you have defined the integer data type in the TYPE section of the program.
These examples all allocate storage for uninitialized arrays. You may also specify that the elements of the arrays be initialized to a single value using declarations like the following in the STATIC and READONLY sections:
RealArray: real32[8] := [ 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0 ]; IntegerAry: integer[8] := [ 1, 1, 1, 1, 1, 1, 1, 1 ];These definitions both create arrays with eight elements. The first definition initializes each four-byte real value to 1.0, the second declaration initializes each integer element to one. Note that the number of constants within the square brackets must match the size you declare for the array.
This initialization mechanism is fine if you want each element of the array to have the same value. What if you want to initialize each element of the array with a (possibly) different value? No sweat, just specify a different set of values in the list surrounded by the square brackets in the example above:
RealArray: real32[8] := [ 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0 ]; IntegerAry: integer[8] := [ 1, 2, 3, 4, 5, 6, 7, 8 ];4.4 HLA Array Constants
The last few examples in the last section demonstrate the use of HLA array constants. An HLA array constant is nothing more than a list of values (all the same time) surrounded by a pair of brackets. The following are all legal array constants:
[ 1, 2, 3, 4 ] [ 2.0, 3.14159, 1.0, 0.5 ] [ `a', `b', `c', `d' ] [ "Hello", "world", "of", "assembly" ](note that this last array constant contains four double word pointers to the four HLA strings appearing elsewhere in memory.)
As you saw in the previous section you can use array constants in the STATIC and READONLY sections to provide initial values for array variables. Of course, the number of comma separated items in an array constant must exactly match the number of array elements in the variable declaration. Likewise, the type of the array constant's elements must match the type of the elements in the array variable.
Using array constants to initialize small arrays is very convenient. Of course, if your array has several thousand elements in it, typing them all in will not be very much fun. Most arrays initialized this way have no more than a couple hundred entries, and generally far less than 100. It is reasonable to use an array constant to initialize such variables. However, at some point it will become far too tedious and error-prone to initialize arrays in this fashion. It is doubtful, for example, that you would want to manually initialize an array with 1,000 different elements using an array constant2. However, if you want to initialize all the elements of an array with the same value, HLA does provide a special array constant syntax for doing so. Consider the following declaration:
BigArray: uns32[ 1000 ] := 1000 dup [ 1 ];This declaration creates a 1,000 element integer array initializing each element of the array with the value one. The "1000 dup [1]" expression tells HLA to create an array constant by duplicating the single value "[ 1 ]" one thousand times. You can even use the DUP operator to duplicate a series of values (rather than a single value) as the following example indicates:
SixteenInts: int32[16] := 4 dup [1,2,3,4];This example initializes SixteenInts with four copies of the sequence "1, 2, 3, 4" yielding a total of sixteen different integers (i.e., 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4 ).
You will see some more possibilities with the DUP operator when looking at multidimensional arrays a little later.
4.5 Accessing Elements of a Single Dimension Array
To access an element of a zero-based array, you can use the simplified formula:
Element_Address = Base_Address + index * Element_Size
For the Base_Address entry you can use the name of the array (since HLA associates the address of the first element of an array with the name of that array). The Element_Size entry is the number of bytes for each array element. If the object is an array of bytes, the Element_Size field is one (resulting in a very simple computation). If each element of the array is a word (or other two-byte type) then Element_Size is two. And so on. To access an element of the SixteenInts array in the previous section, you'd use the formula:
Element_Address = SixteenInts + index*4The 80x86 code equivalent to the statement "EAX:=SixteenInts[index]" is
mov( index, ebx ); shl( 2, ebx ); //Sneaky way to compute 4*ebx mov( SixteenInts[ ebx ], eax );There are two important things to notice here. First of all, this code uses the SHL instruction rather than the INTMUL instruction to compute 4*index. The main reason for choosing SHL is that it was more efficient. It turns out that SHL is a lot faster than INTMUL on many processors.
The second thing to note about this instruction sequence is that it does not explicitly compute the sum of the base address plus the index times two. Instead, it relies on the indexed addressing mode to implicitly compute this sum. The instruction "mov( SixteenInts[ ebx ], eax );" loads EAX from location SixteenInts+EBX which is the base address plus index*4 (since EBX contains index*4). Sure, you could have used
lea( eax, SixteenInts ); mov( index, ebx ); shl( 2, ebx ); //Sneaky way to compute 4*ebx add( eax, ebx ); //Compute base address plus index*4 mov( SixteenInts[ ebx ], eax );in place of the previous sequence, but why use five instructions where three will do the same job? This is a good example of why you should know your addressing modes inside and out. Choosing the proper addressing mode can reduce the size of your program, thereby speeding it up.
Of course, as long as we're discussing efficiency improvements, it's worth pointing out that the 80x86 scaled indexed addressing modes let you automatically multiply an index by one, two, four, or eight. Since this current example multiplies the index by four, we can simplify the code even farther by using the scaled indexed addressing mode:
mov( index, ebx ); mov( SixteenInts[ ebx*4 ], eax );Note, however, that if you need to multiply by some constant other than one, two, four, or eight, then you cannot use the scaled indexed addressing modes. Similarly, if you need to multiply by some element size that is not a power of two, you will not be able to use the SHL instruction to multiply the index by the element size; instead, you will have to use INTMUL or some other instruction sequence to do the multiplication.
The indexed addressing mode on the 80x86 is a natural for accessing elements of a single dimension array. Indeed, it's syntax even suggests an array access. The only thing to keep in mind is that you must remember to multiply the index by the size of an element. Failure to do so will produce incorrect results.
Before moving on to multidimensional arrays, a couple of additional points about addressing modes and arrays are in order. The above sequences work great if you only access a single element from the SixteenInts array. However, if you access several different elements from the array within a short section of code, and you can afford to dedicate another register to the operation, you can certainly shorten your code and, perhaps, speed it up as well. Consider the following code sequence:
lea( ebx, SixteenInts ); mov( index, esi ); mov( [ebx+esi*4], eax );Now EBX contains the base address and ESI contains the index value. Of course, this hardly appears to be a good trade-off. However, when accessing additional elements if SixteenInts you do not have to reload EBX with the base address of SixteenInts for the next access. The following sequence is a little shorter than the comparable sequence that doesn't load the base address into EBX:
lea( ebx, SixteenInts ); mov( index, esi ); mov( [ebx+esi*4], eax ); . . //Assumption: EBX is left alone . // through this code. mov( index2, esi ); mov( [ebx+esi*4], eax );This code is slightly shorter because the "mov( [ebx+esi*4], eax);" instruction is slightly shorter than the "mov( SixteenInts[ebx*4], eax);" instruction. Of course the more accesses to SixteenInts you make without reloading EBX, the greater your savings will be. Tricky little code sequences such as this one sometimes pay off handsomely. However, the savings depend entirely on which processor you're using. Code sequences that run faster on one 80x86 CPU might actually run slower on a different CPU. Unfortunately, if speed is what you're after there are no hard and fast rules. In fact, it is very difficult to predict the speed of most instructions on the 80x86 CPUs.
4.5.1 Sorting an Array of Values
Almost every textbook on this planet gives an example of a sort when introducing arrays. Since you've probably seen how to do a sort in high level languages already, it's probably instructive to take a quick look at a sort in HLA. The example code in this section will use a variant of the Bubble Sort which is great for short lists of data and lists that are nearly sorted, but horrible for just about everything else3.
const NumElements:= 16; static DataToSort: uns32[ NumElements ] := [ 1, 2, 16, 14, 3, 9, 4, 10, 5, 7, 15, 12, 8, 6, 11, 13 ]; NoSwap: boolean; . . . // Bubble sort for the DataToSort array: repeat mov( true, NoSwap ); for( mov( 0, ebx ); ebx <= NumElements-2; inc( ebx )) do mov( DataToSort[ ebx*4], eax ); if( eax > DataToSort[ ebx*4 + 4] ) then mov( DataToSort[ ebx*4 + 4 ], ecx ); mov( ecx, DataToSort[ ebx*4 ] ); mov( eax, DataToSort[ ebx*4 + 4 ] ); // Note: EAX contains mov( false, NoSwap ); // DataToSort[ ebx*4 ] endif; endfor; until( NoSwap );The bubble sort works by comparing adjacent elements in an array. The interesting thing to note in this code fragment is how it compares adjacent elements. You will note that the IF statement compares EAX (which contains DataToSort[ebx*4]) against DataToSort[EBX*4 + 4]. Since each element of this array is four bytes (uns32), the index [EBX*4 + 4] references the next element beyond [EBX*4].
As is typical for a bubble sort, this algorithm terminates if the innermost loop completes without swapping any data. If the data is already presorted, then the bubble sort is very efficient, making only one pass over the data. Unfortunately, if the data is not sorted (worst case, if the data is sorted in reverse order), then this algorithm is extremely inefficient. Indeed, although it is possible to modify the code above so that, on the average, it runs about twice as fast, such optimizations are wasted on such a poor algorithm. However, the Bubble Sort is very easy to implement and understand (which is why introductory texts continue to use it in examples). Fortunately, you will learn about more advanced sorts later in this text, so you won't be stuck with it for very long.
1Or some value whose underlying representation is integer, such as character, enumerated, and boolean types.
2In the chapter on Macros and the HLA Run-Time Language you will learn how to automate the initialization of large array objects. So initializing large objects is not completely out of the question.
3Fear not, you'll see some better sorting algorithms in the chapter on procedures and recursion.
|