4.6 Other Data Representations
Of course, we can represent many different objects other than numbers and characters in a computer system. The following subsections provide a brief description of the different real-world data types you might encounter.
4.6.1 Representing Colors on a Video Display
As you're probably aware, color images on a computer display are made up of a series of dots known as pixels (which is short for "picture elements."). Different display modes (depending on the capability of the display adapter) use different data representations for each of these pixels. The one thing in common between these data types is that they control the mixture of the three additive primary colors (red, green, and blue) to form a specific color on the display. The question, of course, is how much of each of these colors do they mix together?
Color depth is the term video card manufacturers use to describe how much red, green, and blue they mix together for each pixel. Modern video cards generally provide three color depths of eight, sixteen, or twenty-four bits, allowing 256, 65536, or over 16 million colors per pixel on the display. This produces images that are somewhat coarse and grainy (eight-bit images) to "Polaroid quality" (16-bit images), on up to "photographic quality" (24-bit images)1.
One problem with these color depths is that two of the three formats do not contain a number of bits that is evenly divisible by three. Therefore, in each of these formats at least one of the three primary colors will have fewer bits than the others. For example, with an eight-bit color depth, two of the colors can have three bits (or eight different shades) associated with them while one of the colors must have only two bits (or four shades). Therefore, when distributing the bits there are three formats possible: 2-3-3 (two bits red, three bits green, and three bits blue), 3-2-3, or 3-3-2. Likewise, with a 16 bit color depth, two of the three colors can have five bits while the third color can have six bits. This lets us generate three different palettes using the bit values 5-5-6, 5-6-5, or 6-5-5. For 24-bit displays, each primary color can have eight bits, so there is an even distribution of the colors for each pixel.
A 24-bit display produces amazingly good results. A 16-bit display produces okay images. Eight-bit displays, to put it bluntly, produce horrible photographic images (they do produce good synthetic images like those you would manipulate with a draw program). To produce better images when using an eight-bit display, most cards provide a hardware palette. A palette is nothing more than an array of 24-bit values containing 256 elements2. The system uses the eight-bit pixel value as an index into this array of 256 values and displays the color associated with the 24-bit entry in the palette table. Although the display can still display only 256 different colors at one time, the palette mechanism lets users select exactly which colors they want to display. For example, they could display 250 shades of blue and six shades of purple if such a mixture produces a better image for them.
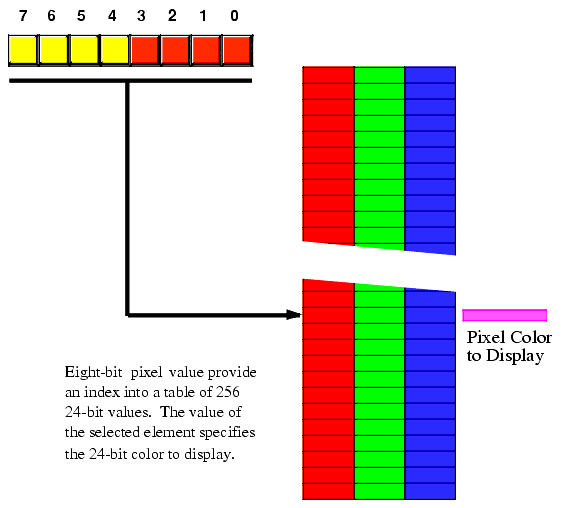
Figure 4.7 Extending the Number of Colors Using a Palette
Unfortunately, the palette scheme only works for displays with minimal color depths. For example, attempting to use a palette with 16-bit images would require a lookup table with 65,536 different three-byte entries - a bit much for today's operating systems (since they may have to reload the palette every time you select a window on the display). Fortunately, the higher bit depths don't require the palette concept as much as the eight-bit color depth.
Obviously, we could dream up other schemes for representing pixel color on the display. Some display systems, for example, use the subtractive primary colors (Cyan, Yellow, and Magenta, plus Black, the so-called CYMK color space). Other display system use fewer or more bits to represent the values. Some distribute the bits between various shades. Monochrome displays typically use one, four, or eight bit pixels to display various gray scales (e.g., two, sixteen, or 256 shades of gray). However, the bit organizations of this section are among the more popular in use by display adapters.
4.6.2 Representing Audio Information
Another real-world quantity you'll often find in digital form on a computer is audio information. WAV files, MP3 files, and other audio formats are quite popular on personal computers. An interesting question is "how do we represent audio information inside the computer?" While many sound formats are far too complex to discuss here (e.g., the MP3 format), it is relatively easy to represent sound using a simple sound data format (something similar to the WAV file format). In this section we'll explore a couple of possible ways to represent audio information; but before we take a look at the digital format, perhaps it's a wise idea to study the analog format first.
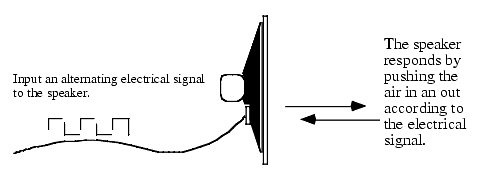
Figure 4.8 Operation of a Speaker
Sounds you hear are the result of vibrating air molecules. When air molecules quickly vibrate back and forth between 20 and 20,000 times per second, we interpret this as some sort of sound. A speaker (see Figure 4.8) is a device which vibrates air in response to an electrical signal. That is, it converts an electric signal which alternates between 20 and 20,000 times per second (Hz) to an audible tone. Alternating a signal is very easy on a computer, all you have to do is apply a logic one to an output port for some period of time and then write a logic zero to the output port for a short period. Then repeat this over and over again. A plot of this activity over time appears in Figure 4.9.
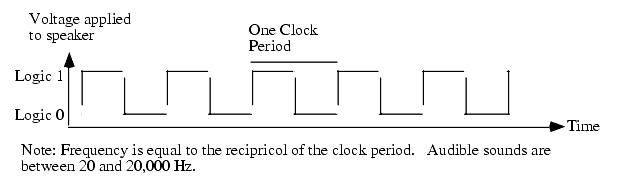
Figure 4.9 An Audible Sound Wave
Although many humans are capable of hearing tones in the range 20-20Khz, the PC's speaker is not capable of faithfully reproducing the tones in this range. It works pretty good for sounds in the range 100-10Khz, but the volume drops off dramatically outside this range. Fortunately, most modern PCs contain a sound card that is quite capable (with appropriate external speakers) of faithfully representing "CD-Quality" sound. Of course, a good question might be "what is CD-Quality sound, anyway?" Well, to answer that question, we've got to decide how we're going to represent sound information in a binary format (see "What is "Digital Audio" Anyway?" on page 112).

Take another look at Figure 4.9. This is a graph of amplitude (volume level) over time. If logic one corresponds to a fully extended speaker cone and logic zero corresponds to a fully retracted speaker cone, then the graph in Figure 4.9 suggests that we are constantly pushing the speaker cone in an out as time progresses. This analog data, by the way, produces what is known as a "square wave" which tends to be a very bright sound at high frequencies and a very buzzy sound at low frequencies. One advantage of a square wave tone is that we only need to alternate a single bit of data over time in order to produce a tone. This is very easy to do and very inexpensive. These two reasons are why the PC's built-in speaker (not the sound card) uses exactly this technique for producing beeps and squawks.
To produce different tones with a square wave sound system is very easy. All you've got to do is write a one and a zero to some bit connected to the speaker somewhere between 20 and 20,000 times per second. You can even produce "warbling" sounds by varying the frequency at which you write those zeros and ones to the speaker.
One easy data format we can develop to represent digitized (or, should we say, "binarized") audio data is to create a stream of bits that we feed to the speaker every 1/40,000 seconds. By alternating ones and zeros in this bit stream, we get a 20 KHz tone (remember, it takes a high and a low section to give us one clock period, hence it will take two bits to produce a single cycle on the output). To get a 20 Hz tone, you would create a bit stream that alternates between 1,000 zeros and 1,000 ones. With 1,000 zeros, the speaker will remain in the retracted position for 1/40 seconds, following that with 1,000 ones leaves the speaker in the fully extended position for 1/40 seconds. The end result is that the speaker moves in and out 20 times a second (giving us our 20 Hz frequency). Of course, you don't have to emit a regular pattern of zeros and ones. By varying the positions of the ones and zeros in your data stream you can dramatically affect the type of sound the system will produce.
The length of your data stream will determine how long the sound plays. With 40,000 bits, the sound will play for one second (assuming each bit's duration is 1/40,000 seconds). As you can see, this sound format will consume 5,000 bytes per second. This may seem like a lot, but it's relatively modest by digital audio standards.
Unfortunately, square waves are very limited with respect to the sounds they can produce and are not very high fidelity (certainly not "CD-Quality"). Real analog audio signals are much more complex and you cannot represent them with two different voltage levels on a speaker. Figure 4.10 provides a typical example of an audio waveform. Notice that the frequency and the amplitude (the height of the signal) varies considerably over time. To capture the height of the waveform at any given point in time we will need more than two values; hence, we'll need more than a single bit.
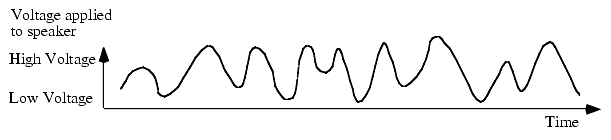
Figure 4.10 A Typical Audio Waveform
An obvious first approximation is to use a byte, rather than a single bit, to represent each point in time on our waveform. We can convert this byte data to an analog signal using a "digital to analog converter" (how obvious) or DAC. This accepts some binary number as input and produces an analog voltage on its output. This allows us to represent an impressive 256 different voltage levels in the waveform. By using eight bits, we can produce a far wider range of sounds than are possible with a single bit. Of course, our data stream now consumes 40,000 bytes per second; quite a big step up from the 5,000 bytes/second in the previous example, but still relatively modest in terms of digital audio data rates.
You might think that 256 levels would be sufficient to produce some impressive audio. Unfortunately, our hearing is logarithmic in nature and it takes an order of magnitude difference in signal for a sound to appear just a little bit louder. Therefore, our 256 different analog levels aren't as impressive to our ears. Although you can produce some decent sounds with an eight-bit data stream, it's still not high fidelity and certainly not "CD-Quality" audio.
The next obvious step up the ladder is a 16-bit value for each point of our digital audio stream. With 65,536 different analog levels we finally reach the realm of "CD-Quality" audio. Of course, we're now consuming 80,000 bytes per second to achieve this! For technical reasons, the Compact Disc format actually requires 44,100 16-bit samples per second. For a stereo (rather than monaural) data stream, you need two 16-bit values each 1/44,100 seconds. This produces a whopping data rate of over 160,000 bytes per second. Now you understand the claim a littler earlier that 5,000 bytes per second is a relatively modest data rate.
Some very high quality digital audio systems use 20 or 24 bits of information and record the data at a higher frequency than 44.1 KHz (48 KHz is popular, for example). Such data formats record a better signal at the expense of a higher data rate. Some sound systems don't require anywhere near the fidelity levels of even a CD-Quality recording. Telephone conversations, for example, require only about 5,000 eight-bit samples per second (this, by the way, is why phone modems are limited to approximately 56,000 bits per second, which is about 5,000 bytes per second plus some overhead). Some common "digitizing" rates for audio include the following:
- Eight-bit samples at 11 KHz
- Eight-bit samples at 22 KHz
- Eight-bit samples at 44.1 KHz
- 16-bit samples at 32 KHz
- 16-bit samples at 44.1 KHz
- 16-bit samples at 48 KHz
- 24-bit samples at 44.1 KHz (generally in professional recording systems)
- 24-bit samples at 48 KHz (generally in professional recording systems)
The fidelity increases as you move down this list.
The exact format for various audio file formats is way beyond the scope of this text since many of the formats incorporate data compression. Some simple audio file formats like WAV and AIFF consist of little more than the digitized byte stream, but other formats are nearly indecipherable in their complexity. The exact nature of a sound data type is highly dependent upon the sound hardware in your system, so we won't delve any farther into this subject. There are several books available on computer audio and sound file formats if you're interested in pursuing this subject farther.
4.6.3 Representing Musical Information
Although it is possible to compress an audio data stream somewhat, high-quality audio will consume a large amount of data. CD-Quality audio consumes just over 160 Kilobytes per second, so a CD at 650 Megabytes holds enough data for just over an hour of audio (in stereo). Earlier, you saw that we could use a palette to allow higher quality color images on an eight-bit display. An interesting question is "can we create a sound palette to let us encode higher quality audio?" Unfortunately, the general answer is no because audio information is much less redundant than video information and you cannot produce good results with rough approximation (which using a sound palette would require). However, if you're trying to produce a specific sound, rather than trying to faithfully reproduce some recording, there are some possibilities open to you.
The advantage to the digitized audio format is that it records everything. In a music track, for example, the digital information records all the instruments, the vocalists, the background noise, and, well, everything. Sometimes you might not need to retain all this information. For example, if all you want to record is a keyboard player's synthesizer, the ability to record all the other audio information simultaneously is not necessary. In fact, with an appropriate interface to the computer, recording the audio signal from the keyboard is completely unnecessary. A far more cost-effective approach (from a memory usage point of view) is to simply record the notes the keyboardist plays (along with the duration of each note and the velocity at which the keyboardist plays the note) and then simply feed this keyboard information back to the synthesizer to play the music at a later time. Since it only takes a few bytes to record each note the keyboardist plays, and the keyboardist generally plays fewer than 100 notes per second, the amount of data needed to record a complex piece of music is tiny compared to a digitized audio recording of the same performance.
One very popular format for recording musical information in this fashion is the MIDI format (MIDI stands for Musical Instrument Digital Interface and it specifies how to connect musical instruments, computers, and other equipment together). The MIDI protocol uses multi-byte values to record information about a series of instruments (a simple MIDI file can actually control up to 16 or more instruments simultaneously).
Although the internal data format of the MIDI protocol is beyond the scope of this chapter, it is interesting to note that a MIDI command is effectively equivalent to a "palette look-up" for an audio signal. When a musical instrument receives a MIDI command telling it to play back some note, that instrument generally plays back some waveform stored in the synthesizer.
Note that you don't actually need an external keyboard/synthesizer to play back MIDI files. Most sound cards contain software that will interpret MIDI commands and play the accompany notes. These cards definitely use the MIDI command as an index into a "wave table" (short for waveform lookup table) to play the accompanying sound. Although the quality of the sound these cards reproduce is often inferior to that a professional synthesizer produces, they do let you play MIDI files without purchasing an expensive synthesizer module3.
If you're interested in the actual data format that MIDI uses, there are dozens of texts available on the MIDI format. Any local music store should carry several of these. You should also be able to find lots of information on MIDI on the Internet (try Roland's web site as a good starting point).
4.6.4 Representing Video Information
Recent increases in disk space, computer speed, and network access have allowed an explosion in the popularity of multimedia on personal computers. Although the term "multimedia" suggests that the data format deals with many different types of media, most people use this term to describe digital video recording and playback on a computer system. In fact, most multimedia formats support at least two mediums: video and audio. The more popular formats like Apple's Quicktime support other concurrent media streams as well (e.g., a separate subtitle track, time codes, and device control). To simplify matters, we limit the discussion in this section to digital video streams.
Fundamentally, a video image is nothing more than a succession of still pictures that the system displays at some rate like 30 images per second. Therefore, if we want to create a digitized video image format, all we really need to do is store 30 or so pictures for each second of video we wish to view. This may not seem like a big deal, but consider that a typical "full screen" video display has 640x480 pixels or a total of 307,200 pixels. If we use a 24-bit RGB color space, then each pixel will require three bytes, raising the total to 921,600 bytes per image. Displaying 30 of these images per second means our video format will consume 27,648,000 bytes per second. Digital audio, at 160 Kilobytes per second is virtually nothing compared to the data requirements for digital video.
Although computer systems and hard disk systems have advanced tremendously over the past decade, maintaining a 30 MByte/second data rate from disk to display is a little too much to expect from all but the most expensive workstations currently available (at least, in the year 2000 as this was written). Therefore, most multimedia systems use various techniques (or combinations of these techniques) to get the data rate down to something more reasonable. In stock computer systems, a common technique is to display a 320x240 quarter screen image rather than a full-screen 640x480 image. This reduces the data rate to about seven megabytes per second.
Another technique digital video formats use is to compress the video data. Video data tends to contain lots of redundant information that the system can eliminate through the use of compression. The popular DV format for digital video camcorders, for example, compresses the data stream by almost 90%, requiring only a 3.3 MByte/second data rate for full-screen video. This type of compression is not without cost. There is a detectable, though slight, loss in image quality when employing DV compression on a video image. Nevertheless, this compression makes it possible to deal with digital video data streams on a contemporary computer system. Compressed data formats are a little beyond the scope of this chapter; however, by the time you finish this text you should be well-prepared to deal with compressed data formats. Programmers writing video data compression algorithms often use assembly language because compression and decompression algorithms need to be very fast to process a video stream in real time. Therefore, keep reading this text if you're interested in working on these types of algorithms.
4.6.5 Where to Get More Information About Data Types
Since there are many ways to represent a particular real-world object inside the computer, and nearly an infinite variety of real-world objects, this text cannot even begin to cover all the possibilities. In fact, one of the most important steps in writing a piece of computer software is to carefully consider what objects the software needs to represent and then choose an appropriate internal representation for that object. For some objects or processes, an internal representation is fairly obvious; for other objects or processes, developing an appropriate data type representation is a difficult task. Although we will continue to look at different data representations throughout this text, if you're really interested in learning more about data representation of real world objects, activities, and processes, you should consult a good "Data Structures and Algorithms" textbook. This text does not have the space to treat these subjects properly (since it still has to teach assembly language). Most texts on data structures present their material in a high level language. Adopting this material to assembly language is not difficult, especially once you've digested a large percentage of this text. For something a little closer to home, you might consider reading Knuth's "The Art of Computer Programming" that describes data structures and algorithms using a synthetic assembly language called MIX. Although MIX isn't the same as HLA or even x86 assembly language, you will probably find it easier to convert algorithms in this text to x86 than it would be to convert algorithms written in Pascal, Java, or C++ to assembly language.
4.7 Putting It All Together
Perhaps the most important fact this chapter and the last chapter present is that computer programs all use strings of binary bits to represent data internally. It is up to an application program to distinguish between the possible representations. For example, the bit string %0100_0001 could represent the numeric value 65, an ASCII character (`A'), or the mantissa portion of a floating point value ($41). The CPU cannot and does not distinguish between these different representations, it simply processes this eight-bit value as a bit string and leaves the interpretation of the data to the application.
Beginning assembly language programmers often have trouble comprehending that they are responsible for interpreting the type of data found in memory; after all, one of the most important abstractions that high level languages provide is to associate a data type with a bit string in memory. This allows the compiler to do the interpretation of data representation rather than the programmer. Therefore, an important point this chapter makes is that assembly language programmers must handle this interpretation themselves. The HLA language provides built-in data types that seem to provide these abstractions, but keep in mind that once you've loaded a value into a register, HLA can no longer interpret that data for you, it is your responsibility to use the appropriate machine instructions that operate on the specified data.
One small amount of checking that HLA and the CPU does enforce is size checking - HLA will not allow you to mix sizes of operands within most instructions4. That is, you cannot specify a byte operand and a word operand in the same instruction that expects its two operands to be the same size. However, as the following program indicates, you can easily write a program that treats the same value as completely different types.
program dataInterpretation; #include( "stdlib.hhf" ); static r: real32 := -1.0; begin dataInterpretation; stdout.put( "`r' interpreted as a real32 value: ", r:5:2, nl ); stdout.put( "`r' interpreted as an uns32 value: " ); mov( r, eax ); stdout.putu32( eax ); stdout.newln(); stdout.put( "`r' interpreted as an int32 value: " ); mov( r, eax ); stdout.puti32( eax ); stdout.newln(); stdout.put( "`r' interpreted as a dword value: $" ); mov( r, eax ); stdout.putd( eax ); stdout.newln(); end dataInterpretation; Program 4.4 Interpreting a Single Value as Several Different Data TypesAs this sample program demonstrates, you can get completely different results by interpreting your data differently during your program's execution. So always remember, it is your responsibility to interpret the data in your program. HLA helps a little by allowing you to declare data types that are slightly more abstract than bytes, words, or double words; HLA also provides certain support routines, like stdout.put, that will automatically interpret these abstract data types for you; however, it is generally your responsibility to use the appropriate machine instructions to consistently manipulate memory objects according to their data type.
1Some graphic artists would argue that 24 bit images are not of a sufficient quality. There are some display/printer./scanner devices capable of working with 32-bit, 36-bit, and even 48-bit images; if, of course, you're willing to pay for them.
2Actually, the color depth of each palette entry is not necessarily fixed at 24 bits. Some display devices, for example, use 18-bit entries in their palette.
3For those who would like a better MIDI experience using a sound card, some synthesizer manufacturers produce sound cards with an integrated synthesizer on-board.
4The sign and zero extension instructions are an obvious exception, though HLA still checks the operand sizes to ensure they are appropriate.
|