TOC PREV NEXT INDEX

Webster Home Page

3.12 Bit Fields and Packed Data

Although the 80x86 operates most efficiently on byte, word, and double word data types, occasionally you'll need to work with a data type that uses some number of bits other than eight, 16, or 32. For example, consider a date of the form "04/02/01". It takes three numeric values to represent this date: a month, day, and year value. Months, of course, take on the values 1..12. It will require at least four bits (maximum of sixteen different values) to represent the month. Days range between 1..31. So it will take five bits (maximum of 32 different values) to represent the day entry. The year value, assuming that we're working with values in the range 0..99, requires seven bits (which can be used to represent up to 128 different values). Four plus five plus seven is 16 bits, or two bytes. In other words, we can pack our date data into two bytes rather than the three that would be required if we used a separate byte for each of the month, day, and year values. This saves one byte of memory for each date stored, which could be a substantial saving if you need to store a lot of dates. The bits could be arranged as shown in the following figure:



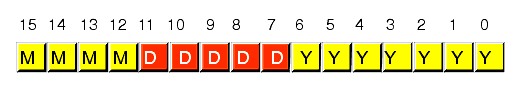
Figure 3.20 Short Packed Date Format (Two Bytes)

MMMM represents the four bits making up the month value, DDDDD represents the five bits making up the day, and YYYYYYY is the seven bits comprising the year. Each collection of bits representing a data item is a bit field. April 2nd, 2001 would be represented as $4101: 

		0100		00010 0000001				= %0100_0001_0000_0001 or $4101
 
		 4		2		01

Although packed values are space efficient (that is, very efficient in terms of memory usage), they are computationally inefficient (slow!). The reason? It takes extra instructions to unpack the data packed into the various bit fields. These extra instructions take additional time to execute (and additional bytes to hold the instructions); hence, you must carefully consider whether packed data fields will save you anything. The following sample program demonstrates the effort that must go into packing and unpacking this 16-bit date format: 


 
program dateDemo;
 

 
#include( "stdlib.hhf" );
 

 
static
 
    day:        uns8;
 
    month:      uns8;
 
    year:       uns8;
 
    
 
    packedDate: word;
 
    
 
begin dateDemo;
 

 
    stdout.put( "Enter the current month, day, and year: " );
 
    stdin.get( month, day, year );
 
    
 
    // Pack the data into the following bits:
 
    //
 
    //  15 14 13 12 11 10  9  8  7  6  5  4  3  2  1  0
 
    //   m  m  m  m  d  d  d  d  d  y  y  y  y  y  y  y
 
    
 
    mov( 0, ax );
 
    mov( ax, packedDate );  //Just in case there is an error.
 
    if( month > 12 ) then
 
    
 
        stdout.put( "Month value is too large", nl );
 
        
 
    elseif( month = 0 ) then
 
    
 
        stdout.put( "Month value must be in the range 1..12", nl );
 
        
 
    elseif( day > 31 ) then
 
    
 
        stdout.put( "Day value is too large", nl );
 
        
 
    elseif( day = 0 ) then
 
    
 
        stdout.put( "Day value must be in the range 1..31", nl );
 
        
 
    elseif( year > 99 ) then
 
    
 
        stdout.put( "Year value must be in the range 0..99", nl );
 
        
 
    else
 
    
 
        mov( month, al );
 
        shl( 5, ax );
 
        or( day, al );
 
        shl( 7, ax );
 
        or( year, al );
 
        mov( ax, packedDate );
 

 
    endif;
 
    
 
    // Okay, display the packed value:
 
    
 
    stdout.put( "Packed data = $", packedDate, nl );
 
    
 
    
 
    
 
    // Unpack the date:
 

 
    mov( packedDate, ax );
 
    and( $7f, al );         // Retrieve the year value.
 
    mov( al, year );
 
    
 
    mov( packedDate, ax );  // Retrieve the day value.
 
    shr( 7, ax );
 
    and( %1_1111, al );
 
    mov( al, day );
 
    
 
    mov( packedDate, ax );  // Retrive the month value.
 
    rol( 4, ax );
 
    and( %1111, al );
 
    mov( al, month );
 

 
    stdout.put( "The date is ", month, "/", day, "/", year, nl );   
 
    
 
        
 
   
 
end dateDemo;
 

 
Program 3.19	 Packing and Unpacking Date Data

Of course, having gone through the problems with Y2K, using a date format that limits you to 100 years (or even 127 years) would be quite foolish at this time. If you're concerned about your software running 100 years from now, perhaps it would be wise to use a three-byte date format rather than a two-byte format. As you will see in the chapter on arrays, however, you should always try to create data objects whose length is an even power of two (one byte, two bytes, four bytes, eight bytes, etc.) or you will pay a performance penalty. Hence, it is probably wise to go ahead and use four bytes and pack this data into a dword variable. Figure 3.21 shows a possible data organization for a four-byte date.



Figure 3.21 Long Packed Date Format (Four Bytes)

In this long packed data format several changes were made beyond simply extending the number of bits associated with the year. First, since there are lots of extra bits in a 32-bit dword variable, this format allots extra bits to the month and day fields. Since these two fields consist of eight bits each, they can be easily extracted as a byte object from the dword. This leaves fewer bits for the year, but 65,536 years is probably sufficient; you can probably assume without too much concern that your software will not still be in use 63 thousand years from now when this date format will wrap around.

Of course, you could argue that this is no longer a packed date format. After all, we needed three numeric values, two of which fit just nicely into one byte each and one that should probably have at least two bytes. Since this "packed" date format consumes the same four bytes as the unpacked version, what is so special about this format? Well, another difference you will note between this long packed date format and the short date format appearing in Figure 3.20 is the fact that this long date format rearranges the bits so the Year is in the H.O. bit positions, the Month field is in the middle bit positions, and the Day field is in the L.O. bit positions. This is important because it allows you to very easily compare two dates to see if one date is less than, equal to, or greater than another date. Consider the following code: 

	mov( Date1, eax );							// Assume Date1 and Date2 are dword variables
 
	if( eax > Date2 ) then							//  using the Long Packed Date format.
 

 
		<< do something if Date1 > Date2 >>
 

 
	endif;

Had you kept the different date fields in separate variables, or organized the fields differently, you would not have been able to compare Date1 and Date2 in such a straight-forward fashion. Therefore, this example demonstrates another reason for packing data even if you don't realize any space savings- it can make certain computations more convenient or even more efficient (contrary to what normally happens when you pack data).

Examples of practical packed data types abound. You could pack eight boolean values into a single byte, you could pack two BCD digits into a byte, etc. Of course, a classic example of packed data is the FLAGs register (see Figure 3.22). This register packs nine important boolean objects (along with seven important system flags) into a single 16-bit register. You will commonly need to access many of these flags. For this reason, the 80x86 instruction set provides many ways to manipulate the individual bits in the FLAGs register. Of course, you can test many of the condition code flags using the HLA @c, @nc, @z, @nz, etc., pseudo-boolean variables in an IF statement or other statement using a boolean expression.

In addition to the condition codes, the 80x86 provides instructions that directly affect certain flags. These instructions include the following:

There are other instructions that affect the FLAGs register as well; these, however, demonstrate how to access several of the packed boolean values in the FLAGs register. The LAHF and SAHF instructions, in particular, provide a convenient way to access the L.O. eight bits of the FLAGs register as an eight-bit byte (rather than as eight separate one-bit values).



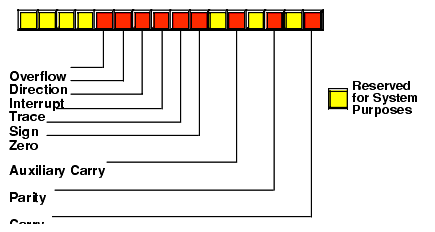
Figure 3.22 The FLAGs Register as a Packed Data Type

The LAHF (load AH with the L.O. eight bits of the FLAGs register) and the SAHF (store AH into the L.O. byte of the FLAGs register) use the following syntax: 

		lahf();
 
		sahf();

3.13 Putting It All Together

In this chapter you've seen how we represent numeric values inside the computer. You've seen how to represent values using the decimal, binary, and hexadecimal numbering systems as well as the difference between signed and unsigned numeric representation. Since we represent nearly everything else inside a computer using numeric values, the material in this chapter is very important. Along with the base representation of numeric values, this chapter discusses the finite bit-string organization of data on typical computer systems, specfically bytes, words, and doublewords. Next, this chapter discusses arithmetic and logical operations on the numbers and presents some new 80x86 instructions to apply these operations to values inside the CPU. Finally, this chapter concludes by showing how you can pack several different numeric values into a fixed-length object (like a byte, word, or doubleword).

Absent from this chapter is any discussion of non-integer data. For example, how do we represent real numbers as well as integers? How do we represent characters, strings, and other non-numeric data? Well, that's the subject of the next chapter, so keep on reading...

Web Site Hits Since
Jan 1, 2000

TOC PREV NEXT INDEX