4.4 Characters
Perhaps the most important data type on a personal computer is the character data type. The term "character" refers to a human or machine readable symbol that is typically a non-numeric entity. In general, the term "character" refers to any symbol that you can normally type on a keyboard (including some symbols that may require multiple key presses to produce) or display on a video display. Many beginners often confuse the terms "character" and "alphabetic character." These terms are not the same. Punctuation symbols, numeric digits, spaces, tabs, carriage returns (enter), other control characters, and other special symbols are also characters. When this text uses the term "character" it refers to any of these characters, not just the alphabetic characters. When this text refers to alphabetic characters, it will use phrases like "alphabetic characters," "upper case characters," or "lower case characters."1.
Another common problem beginners have when they first encounter the character data type is differentiating between numeric characters and numbers. The character `1' is distinct and different from the value one. The computer (generally) uses two different internal, binary, representations for numeric characters (`0', `1', ..., `9') versus the numeric values zero through nine. You must take care not to confuse the two.
Most computer systems use a one or two byte sequence to encode the various characters in binary form. Windows and Linux certainly fall into this category, using either the ASCII or Unicode encodings for characters. This section will discuss the ASCII character set and the character declaration facilities that HLA provides.
4.4.1 The ASCII Character Encoding
The ASCII (American Standard Code for Information Interchange) Character set maps 128 textual characters to the unsigned integer values 0..127 ($0..$7F). Internally, of course, the computer represents everything using binary numbers; so it should come as no surprise that the computer also uses binary values to represent non-numeric entities such as characters. Although the exact mapping of characters to numeric values is arbitrary and unimportant, it is important to use a standardized code for this mapping since you will need to communicate with other programs and peripheral devices and you need to talk the same "language" as these other programs and devices. This is where the ASCII code comes into play; it is a standardized code that nearly everyone has agreed upon. Therefore, if you use the ASCII code 65 to represent the character "A" then you know that some peripheral device (such as a printer) will correctly interpret this value as the character "A" whenever you transmit data to that device.
You should not get the impression that ASCII is the only character set in use on computer systems. IBM uses the EBCDIC character set family on many of its mainframe computer systems. Another common character set in use is the Unicode character set. Unicode is an extension to the ASCII character set that uses 16 bits rather than seven to represent characters. This allows the use of 65,536 different characters in the character set, allowing the inclusion of most symbols in the world's different languages into a single unified character set.
Since the ASCII character set provides only 128 different characters and a byte can represent 256 different values, an interesting question arises: "what do we do with the values 128..255 that one could store into a byte value when working with character data?" One answer is to ignore those extra values. That will be the primary approach of this text. Another possibility is to extend the ASCII character set and add an additional 128 characters to the character set. Of course, this would tend to defeat the whole purpose of having a standardized character set unless you could get everyone to agree upon the extensions. That is a difficult task.
When IBM first created their IBM-PC, they defined these extra 128 character codes to contain various non-English alphabetic characters, some line drawing graphics characters, some mathematical symbols, and several other special characters. Since IBM's PC was the foundation for what we typically call a PC today, that character set has become a pseudo-standard on all IBM-PC compatible machines. Even on modern machines, which are not IBM-PC compatible and cannot run early PC software, the IBM extended character set still survives. Note, however, that this PC character set (an extension of the ASCII character set) is not universal. Most printers will not print the extended characters when using native fonts and many programs (particularly in non-English countries) do not use those characters for the upper 128 codes in an eight-bit value. For these reasons, this text will generally stick to the standard 128 character ASCII character set. However, a few examples and programs in this text will use the IBM PC extended character set, particularly the line drawing graphic characters (see Appendix B).
Should you need to exchange data with other machines which are not PC-compatible, you have only two alternatives: stick to standard ASCII or ensure that the target machine supports the extended IBM-PC character set. Some machines, like the Apple Macintosh, do not provide native support for the extended IBM-PC character set; however you may obtain a PC font which lets you display the extended character set. Other machines have similar capabilities. However, the 128 characters in the standard ASCII character set are the only ones you should count on transferring from system to system.
Despite the fact that it is a "standard", simply encoding your data using standard ASCII characters does not guarantee compatibility across systems. While it's true that an "A" on one machine is most likely an "A" on another machine, there is very little standardization across machines with respect to the use of the control characters. Indeed, of the 32 control codes plus delete, there are only four control codes commonly supported - backspace (BS), tab, carriage return (CR), and line feed (LF). Worse still, different machines often use these control codes in different ways. End of line is a particularly troublesome example. Windows, MS-DOS, CP/M, and other systems mark end of line by the two-character sequence CR/LF. Apple Macintosh, and many other systems mark the end of line by a single CR character. Linux, BeOS, and other UNIX systems mark the end of a line with a single LF character. Needless to say, attempting to exchange simple text files between such systems can be an experience in frustration. Even if you use standard ASCII characters in all your files on these systems, you will still need to convert the data when exchanging files between them. Fortunately, such conversions are rather simple.
Despite some major shortcomings, ASCII data is the standard for data interchange across computer systems and programs. Most programs can accept ASCII data; likewise most programs can produce ASCII data. Since you will be dealing with ASCII characters in assembly language, it would be wise to study the layout of the character set and memorize a few key ASCII codes (e.g., "0", "A", "a", etc.).
The ASCII character set (excluding the extended characters defined by IBM) is divided into four groups of 32 characters. The first 32 characters, ASCII codes 0 through $1F (31), form a special set of non-printing characters called the control characters. We call them control characters because they perform various printer/display control operations rather than displaying symbols. Examples include carriage return, which positions the cursor to the left side of the current line of characters2, line feed (which moves the cursor down one line on the output device), and back space (which moves the cursor back one position to the left). Unfortunately, different control characters perform different operations on different output devices. There is very little standardization among output devices. To find out exactly how a control character affects a particular device, you will need to consult its manual.
The second group of 32 ASCII character codes comprise various punctuation symbols, special characters, and the numeric digits. The most notable characters in this group include the space character (ASCII code $20) and the numeric digits (ASCII codes $30..$39). Note that the numeric digits differ from their numeric values only in the H.O. nibble. By subtracting $30 from the ASCII code for any particular digit you can obtain the numeric equivalent of that digit.
The third group of 32 ASCII characters contains the upper case alphabetic characters. The ASCII codes for the characters "A".."Z" lie in the range $41..$5A (65..90). Since there are only 26 different alphabetic characters, the remaining six codes hold various special symbols.
The fourth, and final, group of 32 ASCII character codes represent the lower case alphabetic symbols, five additional special symbols, and another control character (delete). Note that the lower case character symbols use the ASCII codes $61..$7A. If you convert the codes for the upper and lower case characters to binary, you will notice that the upper case symbols differ from their lower case equivalents in exactly one bit position. For example, consider the character code for "E" and "e" in the following figure:
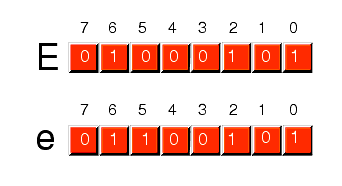
Figure 4.6 ASCII Codes for "E" and "e"
The only place these two codes differ is in bit five. Upper case characters always contain a zero in bit five; lower case alphabetic characters always contain a one in bit five. You can use this fact to quickly convert between upper and lower case. If you have an upper case character you can force it to lower case by setting bit five to one. If you have a lower case character and you wish to force it to upper case, you can do so by setting bit five to zero. You can toggle an alphabetic character between upper and lower case by simply inverting bit five.
Indeed, bits five and six determine which of the four groups in the ASCII character set you're in:
So you could, for instance, convert any upper or lower case (or corresponding special) character to its equivalent control character by setting bits five and six to zero.
Consider, for a moment, the ASCII codes of the numeric digit characters:
The decimal representations of these ASCII codes are not very enlightening. However, the hexadecimal representation of these ASCII codes reveals something very important - the L.O. nibble of the ASCII code is the binary equivalent of the represented number. By stripping away (i.e., setting to zero) the H.O. nibble of a numeric character, you can convert that character code to the corresponding binary representation. Conversely, you can convert a binary value in the range 0..9 to its ASCII character representation by simply setting the H.O. nibble to three. Note that you can use the logical-AND operation to force the H.O. bits to zero; likewise, you can use the logical-OR operation to force the H.O. bits to %0011 (three).
Note that you cannot convert a string of numeric characters to their equivalent binary representation by simply stripping the H.O. nibble from each digit in the string. Converting 123 ($31 $32 $33) in this fashion yields three bytes: $010203, not the correct value which is $7B. Converting a string of digits to an integer requires more sophistication than this; the conversion above works only for single digits.
4.4.2 HLA Support for ASCII Characters
Although you could easily store character values in byte variables and use the corresponding numeric equivalent ASCII code when using a character literal in your program, such agony is unnecessary - HLA provides good support for character variables and literals in your assembly language programs.
Character literal constants in HLA take one of two forms: a single character surrounded by apostrophes or a pound symbol ("#") followed by a numeric constant in the range 0..127 specifying the ASCII code of the character. Here are some examples:
`A' #65 #$41 #%0100_0001Note that these examples all represent the same character (`A') since the ASCII code of `A' is 65.
With a single exception, only a single character may appear between the apostrophes in a literal character constant. That single exception is the apostrophe character itself. If you wish to create an apostrophe literal constant, place four apostrophes in a row (i.e., double up the apostrophe inside the surrounding apostrophes), i.e.,
''''The pound sign operator ("#") must precede a legal HLA numeric constant (either decimal, hexadecimal or binary as the examples above indicate). In particular, the pound sign is not a generic character conversion function; it cannot precede registers or variable names, only constants. As a general rule, you should always use the apostrophe form of the character literal constant for graphic characters (that is, those that are printable or displayable). Use the pound sign form for control characters (that are invisible, or do funny things when you print them) or for extended ASCII characters that may not display or print properly within your source code.
Notice the difference between a character literal constant and a string literal constant in your programs. Strings are sequences of zero or more characters surrounded by quotation marks, characters are surrounded by apostrophes. It is especially important to realize that
`A' ¦ "A"The character constant `A' and the string containing the single character "A" have two completely different internal representations. If you attempt to use a string containing a single character where HLA expects a character constant, HLA will report an error. Strings and string constants will be the subject of a later chapter.
To declare a character variable in an HLA program, you use the char data type. The following declaration, for example, demonstrates how to declare a variable named UserInput:
static UserInput: char;This declaration reserves one byte of storage that you could use to store any character value (including eight-bit extended ASCII characters). You can also initialize character variables as the following example demonstrates:
static TheCharA: char := `A'; ExtendedChar char := #128;Since character variables are eight-bit objects, you can manipulate them using eight-bit registers. You can move character variables into eight-bit registers and you can store the value of an eight-bit register into a character variable.
The HLA Standard Library provides a handful of routines that you can use for character I/O and manipulation; these include stdout.putc, stdout.putcSize, stdout.put, stdin.getc, and stdin.get.
The stdout.putc routine uses the following calling sequence:
stdout.putc( chvar );This procedure outputs the single character parameter passed to it as a character to the standard output device. The parameter may be any char constant or variable, or a byte variable or register3.
The stdout.putcSize routine provides output width control when displaying character variables. The calling sequence for this procedure is
stdout.putcSize( charvar, widthInt32, fillchar );This routine prints the specified character (parameter c) using at least width print positions4. If the absolute value of width is greater than one, then stdout.putcSize prints the fill character as padding. If the value of width is positive, then stdout.putcSize prints the character right justified in the print field; if width is negative, then stdout.putcSize prints the character left justified in the print field. Since character output is usually left justified in a field, the width value will normally be negative for this call. The space character is the most common fill value.
You can also print character values using the generic stdout.put routine. If a character variable appears in the stdout.put parameter list, then stdout.put will automatically print it as a character value, e.g.,
stdout.put( "Character c = `", c, "`", nl );You can read characters from the standard input using the stdin.getc and stdin.get routines. The stdin.getc routine does not have any parameters. It reads a single character from the standard input buffer and returns this character in the AL register. You may then store the character value away or otherwise manipulate the character in the AL register. The following program reads a single character from the user, converts it to upper case if it is a lower case character, and then displays the character:
program charInputDemo; #include( "stdlib.hhf" ); static c:char; begin charInputDemo; stdout.put( "Enter a character: " ); stdin.getc(); if( al >= `a' ) then if( al <= `z' ) then and( $5f, al ); endif; endif; stdout.put ( "The character you entered, possibly ", nl, "converted to upper case, was `" ); stdout.putc( al ); stdout.put( "`", nl ); end charInputDemo; Program 4.1 Character Input SampleYou can also use the generic stdin.get routine to read character variables from the user. If a stdin.get parameter is a character variable, then the stdin.get routine will read a character from the user and store the character value into the specified variable. Here is the program above rewritten to use the stdin.get routine:
program charInputDemo2; #include( "stdlib.hhf" ); static c:char; begin charInputDemo2; stdout.put( "Enter a character: " ); stdin.get(c); if( c >= `a' ) then if( c <= `z' ) then and( $5f, c ); endif; endif; stdout.put ( "The character you entered, possibly ", nl, "converted to upper case, was `", c, "`", nl ); end charInputDemo2; Program 4.2 Stdin.get Character Input SampleAs you may recall from the last chapter, the HLA Standard Library buffers its input. Whenever you read a character from the standard input using stdin.getc or stdin.get, the library routines read the next available character from the buffer; if the buffer is empty, then the program reads a new line of text from the user and returns the first character from that line. If you want to guarantee that the program reads a new line of text from the user when you read a character variable, you should call the stdin.flushInput routine before attempting to read the character. This will flush the current input buffer and force the input of a new line of text on the next input (which should be your stdin.getc or stdin.get call).
The end of line is problematic. Different operating systems handle the end of line differently on output versus input. From the console device, pressing the ENTER key signals the end of a line; however, when reading data from a file you get an end of line sequence which is typically a line feed or a carriage return/line feed pair. To help solve this problem, HLA's Standard Library provides an "end of line" function. This procedure returns true (one) in the AL register if all the current input characters have been exhausted, it returns false (zero) otherwise. The following sample program demonstrates the use of the stdin.eoln function.
program eolnDemo2; #include( "stdlib.hhf" ); begin eolnDemo2; stdout.put( "Enter a short line of text: " ); stdin.flushInput(); repeat stdin.getc(); stdout.putc( al ); stdout.put( "=$", al, nl ); until( stdin.eoln() ); end eolnDemo2; Program 4.3 Testing for End of Line Using Stdin.eolnThe HLA language and the HLA Standard Library provide many other procedures and additional support for character objects. Later chapters in this textbook, as well as the HLA reference documentation, describe how to use these features.
4.4.3 The ASCII Character Set
The following table lists the binary, hexadecimal, and decimal representations for each of the 128 ASCII character codes.
4.5 The UNICODE Character Set
Although the ASCII character set is, unquestionably, the most popular character representation on computers, it is certainly not the only format around. For example, IBM uses the EBCDIC code on many of its mainframe and minicomputer lines. Since EBCDIC appears mainly on IBM's big iron and you'll rarely encounter it on personal computer systems, we will not consider that character set in this text. Another character representation that is becoming popular on small computer systems (and large ones, for that matter) is the Unicode character set. Unicode overcomes two of ASCII's greatest limitations: the limited character space (i.e., a maximum of 128/256 characters in an eight-bit byte) and the lack of international (beyond the USA) characters.
Unicode uses a 16-bit word to represent a single character. Therefore, Unicode supports up to 65,536 different character codes. This is obviously a huge advance over the 256 possible codes we can represent with an eight-bit byte. Unicode is upwards compatible from ASCII. Specifically, if the H.O. 17 bits of a Unicode character contain zero, then the L.O. seven bits represent the same character as the ASCII character with the same character code. If the H.O. 17 bits contain some non-zero value, then the character represents some other value. If you're wondering why so many different character codes are necessary, simply note that certain Asian character sets contain 4096 characters (at least, their Unicode subset).
This text will stick to the ASCII character set except for a few brief mentions of Unicode here and there. Eventually, this text may have to eliminate the discussion of ASCII in favor of Unicode since many new operating systems are using Unicode internally (and convert to ASCII as necessary). Unfortunately, many string algorithms are not as conveniently written for Unicode as for ASCII (especially character set functions) so we'll stick with ASCII in this text as long as possible.
1Upper and lower case characters are always alphabetic characters within this text.
2Historically, carriage return refers to the paper carriage used on typewriters. A carriage return consisted of physically moving the carriage all the way to the right so that the next character typed would appear at the left hand side of the paper.
3If you specify a byte variable or a byte-sized register as the parameter, the stdout.putc routine will output the character whose ASCII code appears in the variable or register.
4The only time stdout.putcSize uses more print positions than you specify is when you specify zero as the width; then this routine uses exactly one print position.
|